I will try to improve the quality of the image below:
Figure 1: photo.jpg
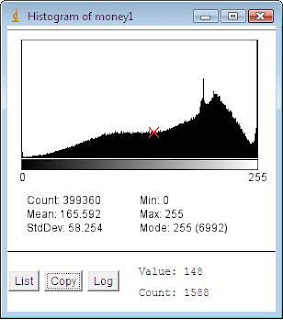
Figure 2: Histogram of photo.jpg using ImageJ
It can be observed from the two figures that the image's quality is poor since a large number of pixels accumulate in a small range of the grayscale values. The image's information are as follows:
FileName: friends.jpg
FileSize: 2865
Format: JPEG
Width: 164
Height: 194
Depth: 8
StorageType: indexed
NumberOfColors: 256
ResolutionUnit: inch
XResolution: 72.000000
YResolution: 72.000000
I. In a separate scipad, I defined the following functions and save it as "myfunc.sce":
-->function [X,Y,L,V,W,Z]=myfunctions(im);
-->X=[];
-->Y=[];
-->L=[];
-->v=1;
-->for i=0:1:255;
-->[x,y]=find(im==i);
-->X(v)=i; // gives the grayscale value
-->Y(v)=length(x); //gives the number of pixels
-->L(v)=(v-128)./255; // this is for the function that will give a theoretical CDF
-->v=v+1;
-->end;
-->V=(0.5.*tanh(5.*L))+1; // Function of the theoretical CDF I wish to obtain later
-->W=Y/c; // normalizes Y
-->Z=cumsum(W); //gives the normalized cumulative sum of Y
-->endfunction;
Figure 2: Histogram of photo.jpg using ImageJIt can be observed from the two figures that the image's quality is poor since a large number of pixels accumulate in a small range of the grayscale values. The image's information are as follows:
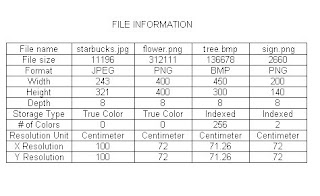
FileName: friends.jpg
FileSize: 2865
Format: JPEG
Width: 164
Height: 194
Depth: 8
StorageType: indexed
NumberOfColors: 256
ResolutionUnit: inch
XResolution: 72.000000
YResolution: 72.000000
I. In a separate scipad, I defined the following functions and save it as "myfunc.sce":
-->function [X,Y,L,V,W,Z]=myfunctions(im);
-->X=[];
-->Y=[];
-->L=[];
-->v=1;
-->for i=0:1:255;
-->[x,y]=find(im==i);
-->X(v)=i; // gives the grayscale value
-->Y(v)=length(x); //gives the number of pixels
-->L(v)=(v-128)./255; // this is for the function that will give a theoretical CDF
-->v=v+1;
-->end;
-->V=(0.5.*tanh(5.*L))+1; // Function of the theoretical CDF I wish to obtain later
-->W=Y/c; // normalizes Y
-->Z=cumsum(W); //gives the normalized cumulative sum of Y
-->endfunction;
II. Now, in Scilab's command window:
-->im=imread('photo.jpg');// loads the image in Scilab
-->a=size(im,1);
-->b=size(im,2);
-->c=a.*b; //gives the total size of the image
-->getf('myfunc.sce'); //gets the function from the file "myfunc.sce" -->[X,Y,L,V,W,Z]=myfunctions(im); // Loads the functions in I
To plot the histogram:
-->plot(X,Y); //plots the histogram
Figure 3: Histogram of photo.jpg
To plot the PDF/normalized histogram:
-->xbasc(); // clears the previous plot in the graphics window
-->plot(X,W);
Figure 4: PDF of photo.jpg
To plot the CDF:
-->xbasc();
-->plot(X,Z); //plots the CDF
Figure 5:CDF of photo.jpg
Figure 6: Theoretical CDF
-->photo1=[];
-->for e=1:1:a;
-->for f=1:1:b;
-->photo1(e,f)=Z(im(e,f));
-->end;
-->end;
-->imwrite(photo1,'photo1.jpg');
Here is the new image:
-->im=imread('photo.jpg');// loads the image in Scilab
-->a=size(im,1);
-->b=size(im,2);
-->c=a.*b; //gives the total size of the image
-->getf('myfunc.sce'); //gets the function from the file "myfunc.sce" -->[X,Y,L,V,W,Z]=myfunctions(im); // Loads the functions in I
To plot the histogram:
-->plot(X,Y); //plots the histogram
Figure 3: Histogram of photo.jpgTo plot the PDF/normalized histogram:
-->xbasc(); // clears the previous plot in the graphics window
-->plot(X,W);
Figure 4: PDF of photo.jpgTo plot the CDF:
-->xbasc();
-->plot(X,Z); //plots the CDF
Figure 5:CDF of photo.jpgTo plot the theoretical CDF:
-->xbasc();
-->plot(X,V); //plots the the theoretical CDF
-->xbasc();
-->plot(X,V); //plots the the theoretical CDF
Figure 6: Theoretical CDFTo enhance the image's quality, I replaced each pixel value by the image's CDF value.
-->photo1=[];
-->for e=1:1:a;
-->for f=1:1:b;
-->photo1(e,f)=Z(im(e,f));
-->end;
-->end;
-->imwrite(photo1,'photo1.jpg');
Here is the new image:
Figure 7: photo1.jpg
III. In a new scilab window, I simply repeated step II and change 'photo.jpg' to 'photo1.jpg' and here are the results:
Figure 8:Histogram of photo1.jpg
Figure 9: PDF of photo1.jpg
Figure 10: CDF photo1.jpg
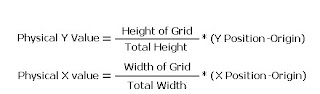
IV. I tried producing a non-linear CDF that will mimic the CD of the human eye. For this part, the function "V=(0.5.*tanh(5.*L))+1" in Step I will serve as the theoretical CDF. I first used the CDF of 'photo.jpg.' For each grayscale value on the x-axis, I need to obtain its corresponding value on the y-axis (See Figure 5). I will then substitute this with the values of theoretical CDF (i.e V, see Figure 6). By taking the inverse of V, a new set of grayscale values were obtained. The result is a new image with a wider range of grayscale values, and hence a better contrast. The codes are written below:
-->im=imread('photo.jpg');
-->a=size(im,1);
-->b=size(im,2);
-->c=a.*b;
-->getf('myfunc.sce');
-->[X,Y,L,V,W,Z]=myfunctions(im);
-->w=[0:255]; // new set of gray scale values
-->//To get the projection of the grayscale value of the untreated image on its CDF I used
-->A=interp1(X,Z,im);
-->//To replace the projection above with the theoretical CDF and project this on a new grayscale value I used
-->B=interp1(V,w,A);
-->C=B./255;
-->imwrite(C,'photo2.jpg');
The resulting image is as follows:
Figure 11: photo2.jpg
V. By repeating step II and substituting 'photo.jpg' by 'photo2.jpg', the plots for the image are below:
Figure 12:Histogram of photo2.jpg
Figure 13: PDF of photo2.jpg
Figure 14: CDF of photo2.jpgIn last two images, the contrast of the image improved because image pixels can be found in all grayscale values. It can also be observed that the last two photos lack "smoothness" in comparison to the original photo. I think that this is due to the peaks found in their histograms. The variation in the length of the peaks causes the non-continuity of the grayscale values in each pixel. But as of the moment, I still can't figure out how to arrange this.
I rate myself 10/10 for this activity.
Photo Source:
http://www.american-indian-artwork.com/restoration/grayscale-picture-650.jpg
